Al 6-lea arbore

Obisnuim sa facem media consumului de carburant la 100 km, media notelor obtinute la scoala sau media orelor petrecute in trafic. Media aritmetica este indicatorul statistic cel mai des folosit in viata de zi cu zi. Este un indicator important pentru foarte multe domenii iar silvicultura nu face exceptie. In silvicultura media arimetica nu este foarte des folosita fiind preferata media patratica. De ce? Deoarece multiplicand volumul arborelui care are diametrul egal cu media patratica a diametrelor cu numarul de arbori la hectar obtinem volumul de lemn al intregului hectar [1]. Deci, daca stim media patratica a diametrelor, inaltimea corespunzatoare acestuia si numarul de arbori putem calcula volumul de lemn, respectiv stocul de carbon, respectiv cat valoreaza acel hectar de padure.

Totusi, un hectar de padure de molid poate sa aiba la varsta de 60 de ani peste 850 de arbori de diferite dimensiuni [2]. Ce ar insemna sa estimam valoarea ecologica, sociala si economica a celor 7 milioane de hectare de padure din Romania calculand media patratica a diametrelor arborilor pentru fiecare hectar? Aceasta problema a fost si inca este de interes pentru multi cercetatori din silvicultura. Astfel, de-a lungul timpului au fost dezvoltate procedee rapide [3] prin care se urmareste determinarea diametrului mediu patratic si a numarului de arbori astfel incat sa fie usurata munca de teren a silvicultorilor.
Calcand pe urmele unor cercetari din trecut am intalnit o teorie interesanta. Regula generala a lui Weise (Weise’s rule of thumb) pentru determinarea diametrului mediu patratic.

Weise prin 1880 propune urmatoarea metoda pentru a determina rapid diametrul mediu patratic al unui hectar de padure. Se masoara cei mai apropiati 10 arbori iar diametrul mediu patratic este egal cu valoarea celui de-al 6-lea diametru din sirul ordonat crescator al celor 10 arbori masurati. Interesant, nu? Practic nu mai trebuie sa masor peste 850 de arbori sa aflu media patratica ci numai 10, pe care sa ii ordonez crescator si dimensiunea celui de-al 6-lea arbore din sir este egala cu diametrul mediu patratic al hectarului.

Pare prea usor ca sa fie adevarat. Haide sa testam ce zice Weise. Pentru a face acest lucru avem nevoie de o suprafata de padure masurata fir cu fir in care arbori au coordonate (X,Y) astfel incat sa putem determina cei mai apropiati 10 arbori de un punct ales la intamplare de noi. In R exista un pachet numit spatstat care are acest gen de informatii.

require(dplyr)
require(ggplot2)
require(reshape2)
require(spatstat)
require(ggthemes)

Pachetul spatstat include un set de date numit Spruces pe care il putem importa si folosi pentru acest tip de analiza. Deoarece de obicei diametrul este exprimat in cm, diametrul arborilor din setul de date a fost transformat din metri in cm.

data("spruces")
spruces[["marks"]]<-spruces[["marks"]]*100
plot(spruces)

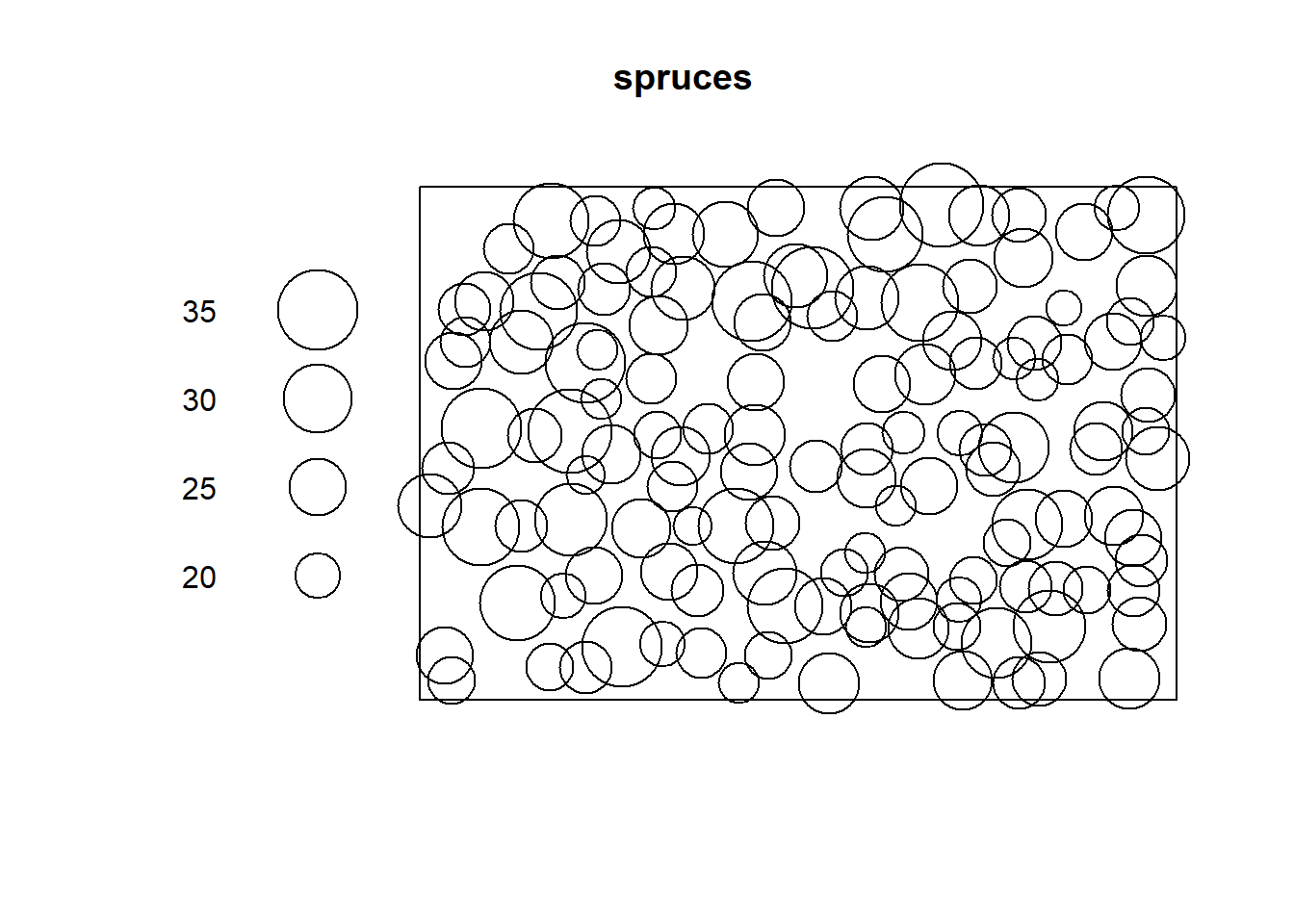Putem observa in graficul de mai sus distributia spatiala a arborilor si dimensiunile acestora in cm.

summary(spruces)

## Marked planar point pattern:  134 points
## Average intensity 0.06296992 points per square metre
## 
## Coordinates are given to 1 decimal place
## i.e. rounded to the nearest multiple of 0.1 metres
## 
## marks are numeric, of type 'double'
## Summary:
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   16.00   22.00   24.50   25.04   27.00   37.00 
## 
## Window: rectangle = [0, 56] x [0, 38] metres
## Window area = 2128 square metres
## Unit of length: 1 metre

Setul de date se refera la o suprafata rectangulara de 2128 m patrati (56 x 38) instalata intr-o padure de molid din Germania unde au fost masurati 134 de arbori. Diametrul minim masurat este de 16 cm, diametrul mediu artimetic este 25 cm iar diametrul maxim este de 37. Pe noi ne intereseaza diametrul mediu patratic care se calculeaza cu urmatoarea formula:

$$ \sqrt{\frac{\sum_{i=1}^{n} d_{i}^2}{n}} $$ unde $ d $ reprezinta diametrul arborelui $ i $ si $ n $ reprezinta numarul total de arbori, in cazul nostru 134.

round(sqrt(sum(spruces[["marks"]]^2)/length(spruces[["marks"]])),2)

## [1] 25.47

Diametrul mediu patratic al setului de date este 25.47 cm.

Mai departe putem folosi functiile implementate in pachetul spatastat pentru a testa daca diametrul celui de-al 6-lea arbore dintr-un sir de 10 arbori este egal cu 25.47. Intrebarea este din ce loc sa extragem cei 10 arbori? Pentru a elimina factorul intamplator putem considera fiecare arbore ca fiind pozitia noastra in suprafata inventariata si extrage cei mai apropiati 10 arbori fata de acel punct. In acest fel testam daca regula lui Weise este valabila indiferent de pozitia noastra in suprafata inventariata obtinand de asemenea 134 de seturi de 10 arbori.

dgmean <- as.data.frame(apply((markstat (spruces, fun=print,N=10)),2,sort))

dg_df<-melt(dgmean[6,])
mm <- dg_df %>% 
              group_by(value) %>% 
              summarise(n = n()) %>% mutate(n_proc=round(n/sum(n)*100,1))

ggplot(data=mm, aes(x=value, y=n)) +
  geom_bar(stat="identity", width=0.5, position=position_dodge(), fill = "steelblue") + 
  geom_text(aes(label=n), vjust=0.9, color="white",
            position = position_dodge(0.9), size=4)+
  geom_vline(xintercept = 25, color="red" )+
  theme_base()+
  labs(x="Diametrul celui de-al 6-lea arbore", y= "Numar de seturi")

In graficul de mai sus putem observa ca in 42 de cazuri diametrul celui de-al 6 lea arbore a fost egal cu 25 de cm adica egal cu diametrul mediu patratic al intregii suprafete inventariate. In 37 de cazuri cel de-al 6 arbore a avut un diametru de 24 iar in 17 cazuri a avut un diametru de 26. Se pare ca Weise are dreptate in cele mai multe cazuri. Chiar daca am lua cele mai rele seturi unde diametrul celui de-al 6-lea arbore a fost egal cu 20 si 28 de cm, aceste valori au o eroare acceptata in cele mai multe lucrari desfasurate in silvicultura.

Totusi, poate rezultatele obtinute sunt intamplatoare, si daca am folosi un alt set de date am obtine alte rezultate.

Pachetul lmfor include un set de date format din 66 de suprafete de pin silvestru din Ilomantsi, Finlanda care are toate informatiile necesare pentru a testa regula lui Weise in toate cele 66 de suprafete. Vom urma aceeasi procedura ca cea de mai sus pentru fiecare dintre cele 66 de suprafete de proba. In plus, vom testa daca diametrul mediu patratic al suprafetei este mai apropiat de diametrul altor arbori din setul de 10 arbori.

require(lmfor)
data("spati")
for (i in 1:length(unique(spati$plot))){
  pl<-unique(spati$plot)[i]
  X <- ppp(spati$xk[spati$plot==pl], spati$yk[spati$plot==pl],
           window=owin(c(0,spati$X[spati$plot==pl][1]),c(0,spati$X[spati$plot==pl][1])),marks = spati$d[spati$plot==pl])
  dgmean <- as.data.frame(apply((markstat (X, fun=print,N=10)),2,sort))
  dgmean$n<-seq(1,10,1)
  dgmean<-reshape2::melt(dgmean, id=c("n"))
  dgmean$plot<-pl
  assign(paste("plot_",pl, sep=""),dgmean)
}

weisse_data<-do.call(rbind.data.frame,mget(ls(pattern = "plot")))
weisse_data<-weisse_data %>% group_by(plot,n) %>% summarise(dg=mean(value)) 
spati_filt<-spati %>% group_by(plot) %>% summarise(Dg=sqrt(sum(d^2)/n()))
weisse<-left_join(weisse_data, spati_filt )
weisse$dif<-abs(weisse$dg-weisse$Dg)
weisse<-weisse %>% group_by(plot) %>% mutate(min= min(dif)) %>% filter(dif==min)
ggplot(weisse, aes(n))+
  geom_histogram(fill = "steelblue")+
  theme_base()+
  labs(x="Numarului arborelui", y="Numarul suprafetelor de proba")

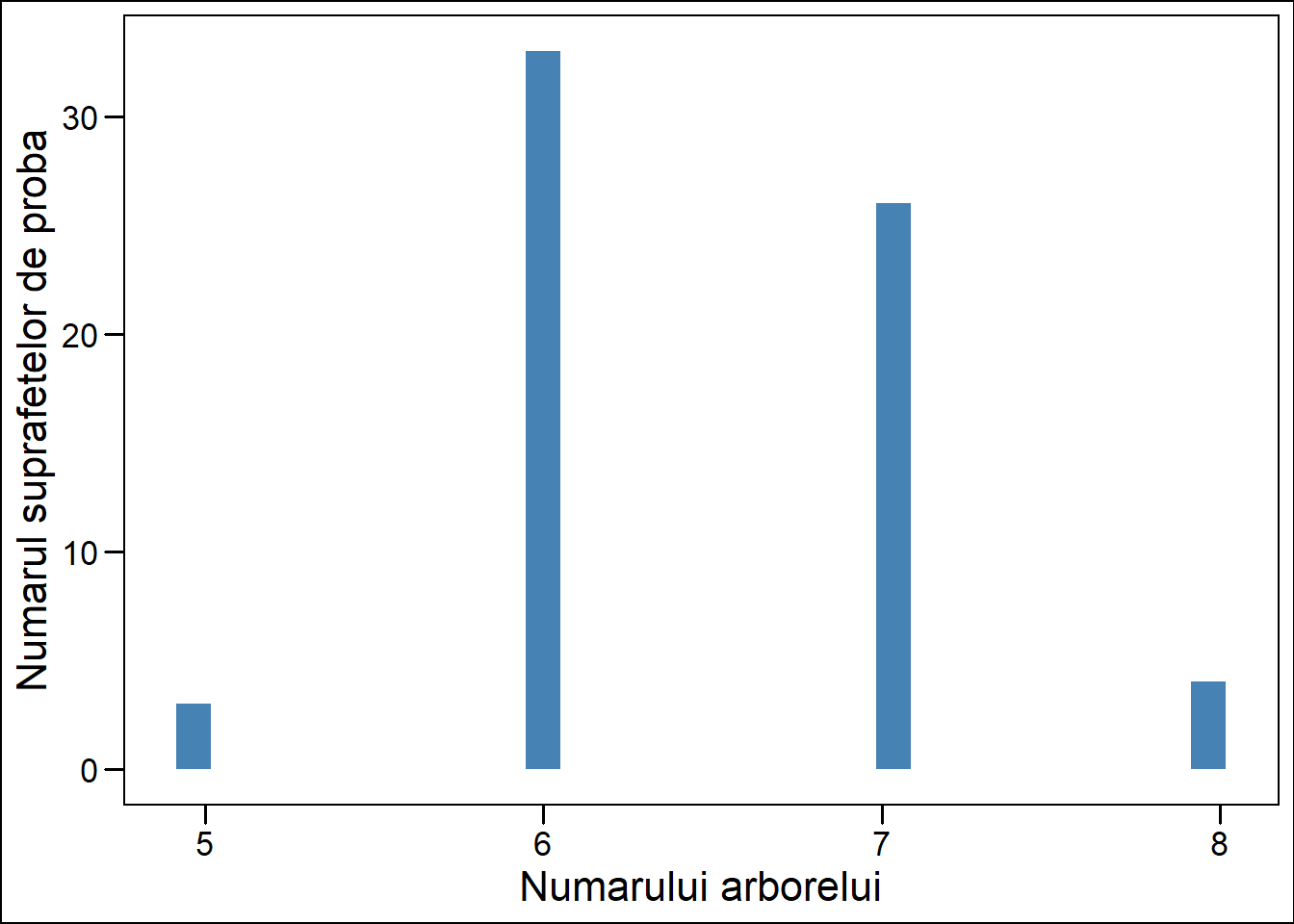
Peste 30 din cele 66 de suprafete au media patratica a diametrelor apropiata de dimensiunea celui de-al 6-lea arbore. Sub 10 suprafete au avut media patratica a diametrelor apropiata de dimensiunea arborilor 5 si 8 si peste 25 de suprafete au avut media patratica a diametrelor apropiata de dimensiunea arborelui 7.

Observam ca nu numai diametrul celui de-al 6-lea arbore poate reprezenta media patratica a unei suprafete. Cand este totusi aplicabila regula lui Weise? Aplicabilitate regulii lui Weise tine de tipul de distrbutie a numarului de arbori pe categorii de diametre din suprafata de interes. Practic acolo unde distributia arborilor pe categorii de diametre este apropiata de distributia normala [4] dimensiunea arborelui 6 va fi egala cu media patratica a diametrelor deoarece valoarea cuantilei 6 din distributia normala este aproximativ egala cu media patratica.
Daca vizualizam distributia arborilor pe categorii de diametre a celor 33 de suprafete unde arborele 6 a avut dimensiunea cea mai apropiata de media patratica a intregii suprafete, observam ca distributiile acestora sunt asemanatoare cu distributia normala.

spati[spati$plot %in% c(weisse$plot[weisse$n==6]),] %>%
  ggplot(aes(d))+
  geom_density()+
  geom_vline(data=weisse[weisse$n==6,],aes(xintercept=Dg),size=0.7, color="blue")+
  geom_vline(data=weisse[weisse$n==6,],aes(xintercept=dg),size=0.7, color="red", linetype=2)+
  facet_wrap(~plot, scales="free")+
  labs(x="Diametrul")+
  theme_bw()

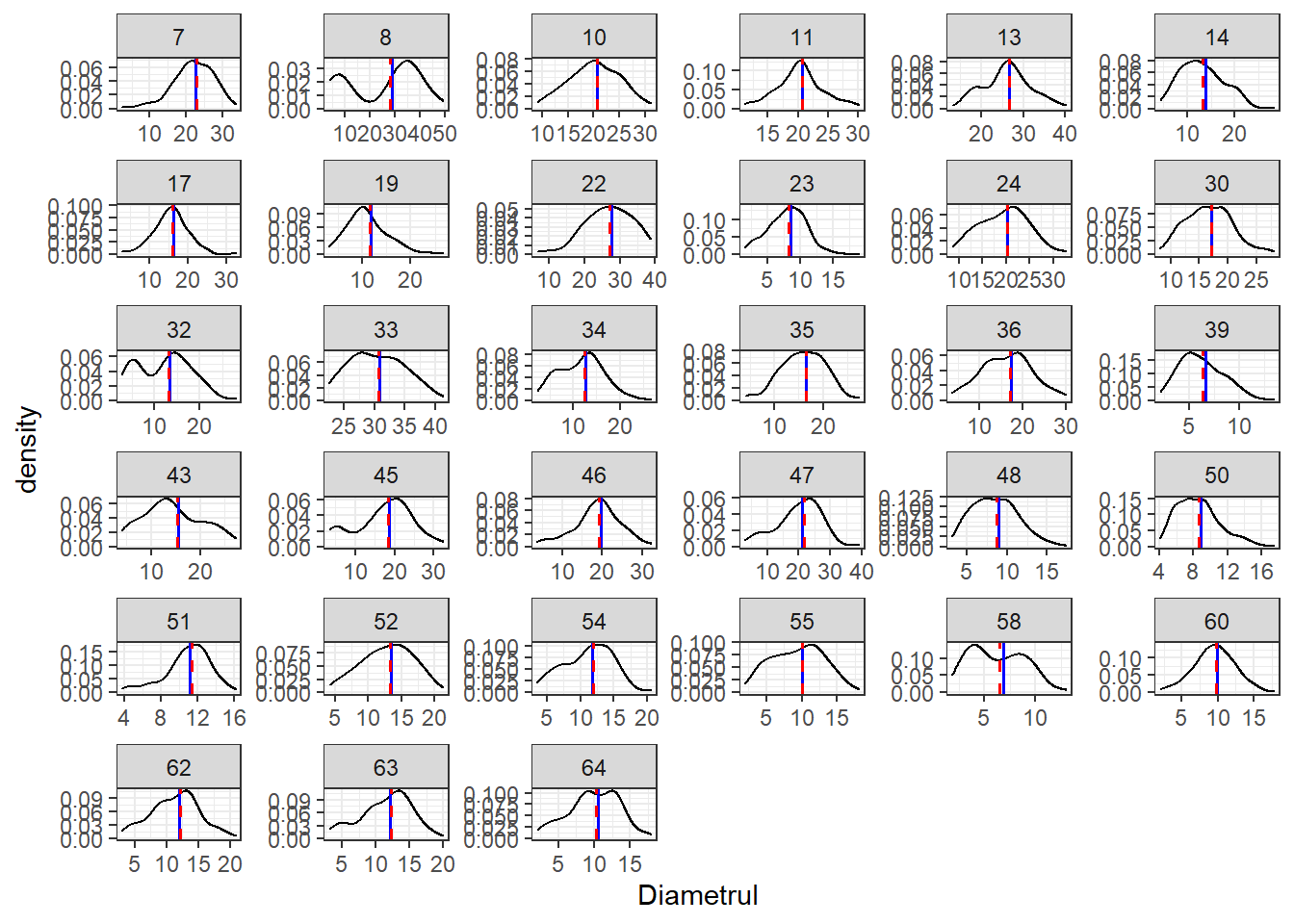Linia verticala albastra reprezinta media patratica a diametrelor aferenta fiecarei suprafete iar linia rosie punctata reprezinta media diametrelor arborelui 6 din cele n seturi de 10 arbori extrase pentru fiecare suprafata. Diferentele sunt nesemnificative in cele mai multe cazuri si putem observa ca majoritatea distributiilor sunt apropiate de distributia normala.

Acolo unde distributia arborilor nu este apropiata de distributia normala cercetarile [5, 6] au demonstrat ca se pot folosi dimensiunile arborelui 5, 7 sau 8. De exemplu acolo unde distributia arborilor pe categorii de diametre are o forma negativ exponentiala se poate folosi diametrul arborelui 8.

spati[spati$plot %in% c(weisse$plot[weisse$n %in% c(8)]),] %>%
  ggplot(aes(d))+
  geom_density()+
  geom_vline(data=weisse[weisse$n==8,],aes(xintercept=Dg),size=0.7, color="blue")+
  geom_vline(data=weisse[weisse$n==8,],aes(xintercept=dg),size=0.7, color="red", linetype=2)+
  facet_wrap(~plot, scales="free")+
  labs(x="Diametrul")+
  theme_bw()

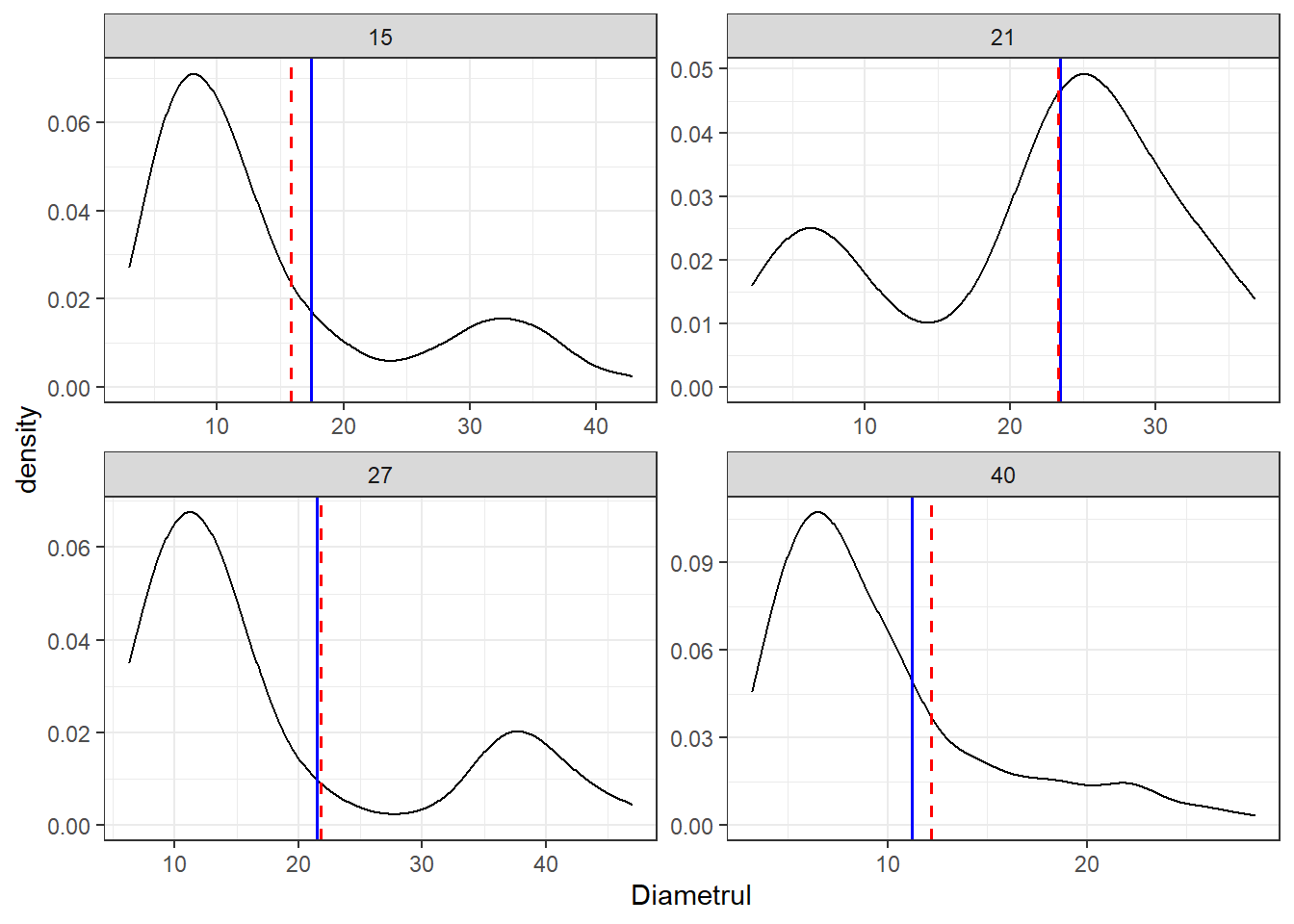
Nu este cazul plotului 21 dar forma distributiei numarului de arbori pe categorii de diametre in celalalte ploturi este similara cu cea negativ exponentiala. Dupa cum se poate observa in graficul de mai jos erorile asociate acestei metode sunt reduse de pana la 1.5 cm. Aceasta metoda este implementata pentru determinarea rapida a diametrului mediu patratic in amenajarea padurilor in Slovacia sau Cehia stabilindu-se pentru fiecare tip de padure numarul arborelui care estimeaza cel mai bine media arboretelor.

ggplot(weisse, aes(factor(n), dif, group=n,fill=factor(n)))+
  geom_boxplot(show.legend = FALSE)+
  labs(x="Numarul arborelui", y="Diferenta dintre diametrului arborelui si\n media patratica a plotului (cm)")+
  theme_bw()

O lucrare mai recenta [7] vine cu o imbunatatire a regulii lui Weise. Cercetatorii demonstreaza ca media artimetica a diametrelor arborilor 6 si 7, 4 si 8 sau 3 si 9 reprezinta o mai buna estimare a diametrului mediu patratic decat diametrul arborelui 6.
In orice caz, mi se pare fascinant cum la 1880, Weise reuseste sa formuleze aceasta regula. Oare in ce alte domenii se poate folosi sau este deja utilizata aceasta legitate?

Referinte

1. Curtis, R. O., & Marshall, D. D. (2000). Why quadratic mean diameter?. Western Journal of Applied Forestry, 15(3), 137-139.
2. Giurgiu, V., & Draghiciu, D. (2004). Modele matematico-auxologice si tabele de productie pentru arborete. Editura Ceres, Bucuresti, 607.
3. Giurgiu, V. (1979). Dendrometrie si auxologie forestiera. Ceres.
4. Patel, J. K., & Read, C. B. (1996). Handbook of the normal distribution (Vol. 150). CRC Press.
5. Halaj, J. Mathematical and statistical survey of diameter structure of Slovak stands. Les. Cas. For. J. 1957, 3, 39-74.
6. Collective. Technical Guidelines for Forest Management; Institute for Forest Management: Zvolen, Slovakia, 1984; p. 594.
7. Sedmak, R., Scheer, L., Marusak, R., Bosela, M., Sedmakova, D., & Fabrika, M. (2015). An improved Weise’s rule for efficient estimation of stand quadratic mean diameter. Forests, 6(8), 2545-2559.